Ha! Maybe not. Doing them can be hard, but now analyzing them on rowsandall is easy.
One of the “Pro” features that rowsandall has had for a long time is the ability to divide up a workout into work intervals and rest intervals. Now, Sander has added the ability to slice a workout into work and rest intervals by using a threshold, either pace, power or work per stroke.
Why is this a good thing?
- On the erg, the PM provides the ability to program interval workouts, and these intervals are accurately represented in the online logbook, but neither the data export from the logbook nor the export from painsled preserve the exact interval structure. Once you have this data in rowsandall, you need to redefine the intervals.
- This is also true for on the water intervals, but there is an even more important problem, at least for me. I find that it is really hard to use preprogrammed intervals on the water because of location, river geography, boat traffic, or safety concerns. I will often need to extend or cut short a rest, and if I get waked, I might want to extend the interval . For that reason, I tend to row interval workouts as a “just row” session and note the end time or distance at the start of each interval that I am rowing to. In this case, you need to have a way to easily pick out the work from the rest.
Blocking a workout into work and rest unleashes the power of rowsandall. Most of the analytical tools are “rest aware”. So, when you get a summary of a workout you can see your stats for each interval, and for the total of all the work intervals.
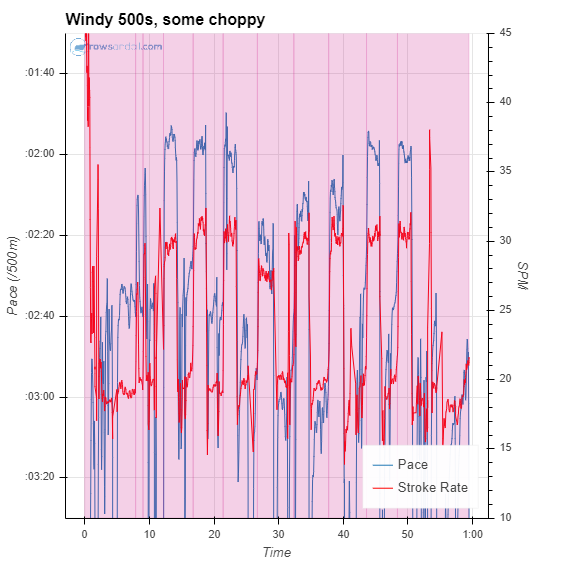
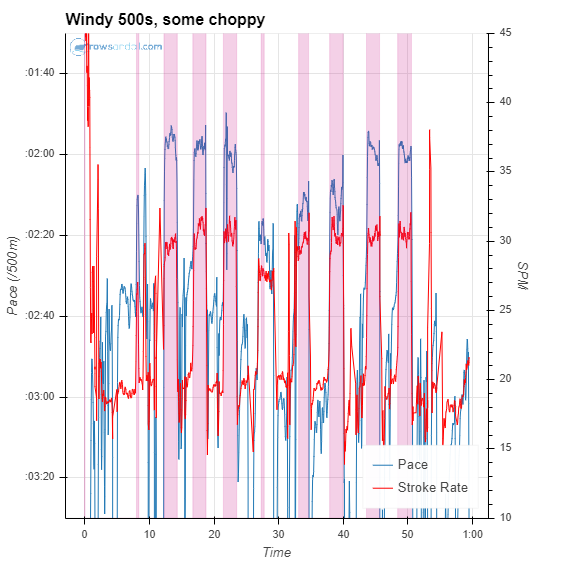
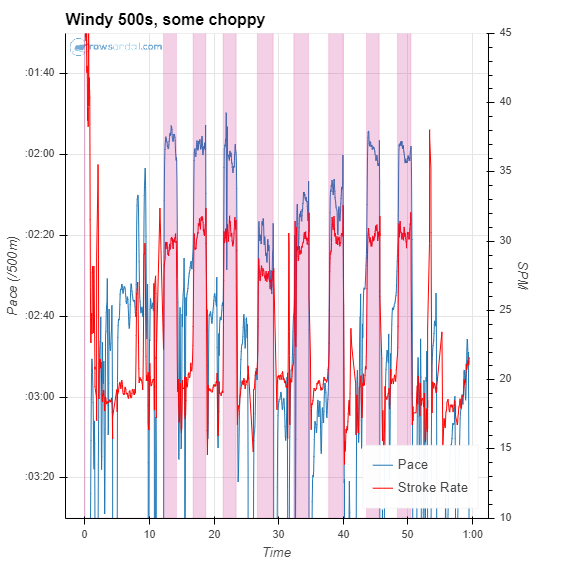
It’s easiest to see in an example. Last Wednesday, I was doing a tough workout. The training plan called for 4 x (2′ @ race pace / 1′ paddle / 2′ @ race pace) / 4′ rest. I set up the speedcoach for a just row session and took off. I started as I usually do with a King of the Mountain drill, then a pick drill, then the OTW warmup that I learned when I was doing Rojabo. That took me down to the end of the river. Then it was time for the workout. I row on a twisty river, so I wanted to make sure that I would have a nice straight section in front of me for each 2′ section. So, I wanted to adjust my start and stop times as needed to get set up. Here’s the plot of workout.
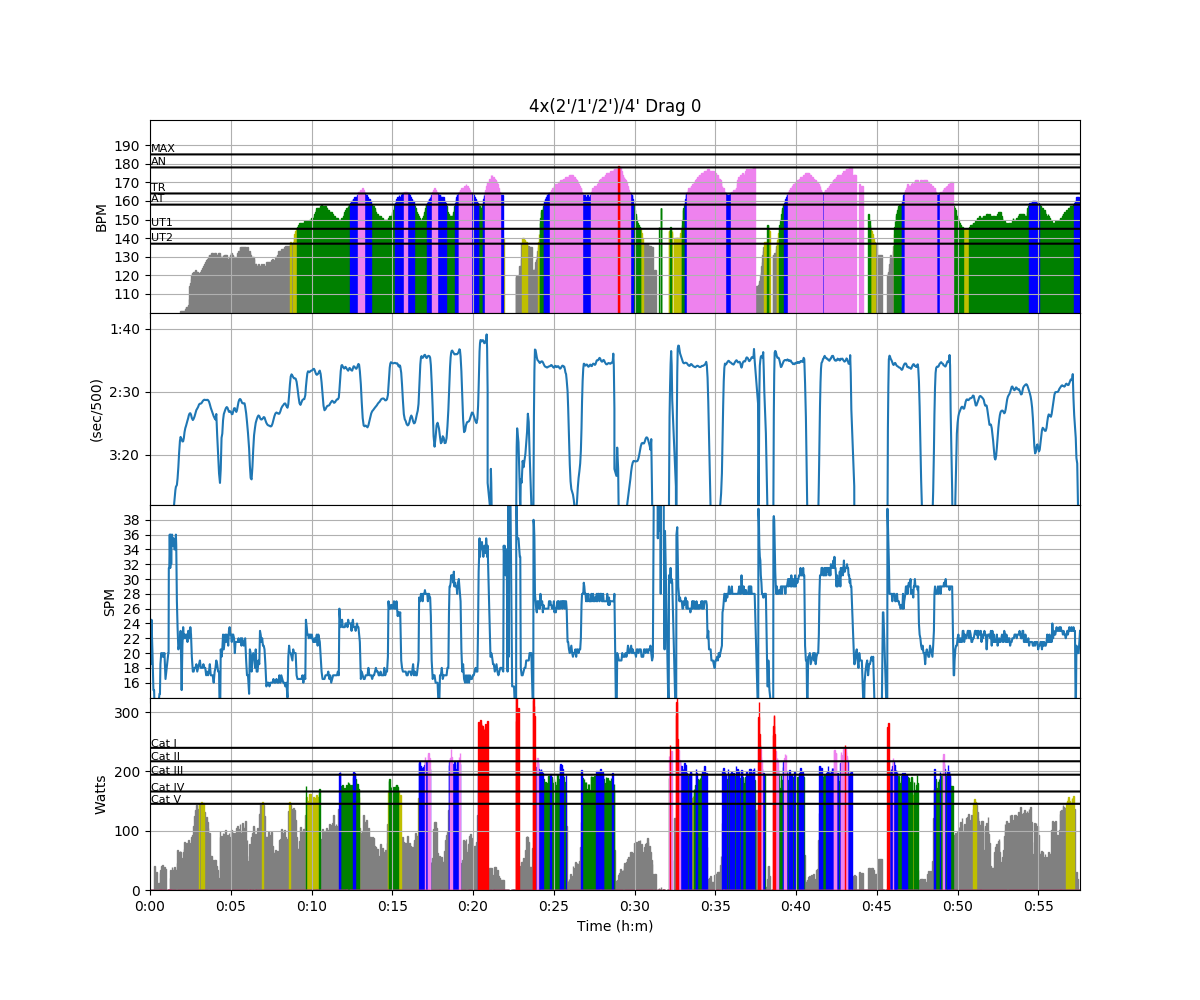
You can see all sorts of weird stuff going on. The first set looks ok, but the second one, I wasn’t happy with my start, so I started again. The same thing happened with the beginning of the third set. The fourth set was going fine, but my will to continue left me with less than a minute left and a cut it short.
Now, trying to sort out the intervals for a session like this used to be a real chore. Now it is easy. I just select Intervals in the context menu on the left, whenever I am editing a workout.
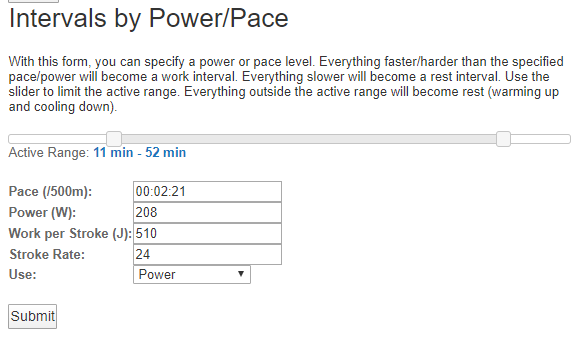
Then on the Edit Intervals page, scroll all the way down to find the “Intervals by Power/Pace” section.
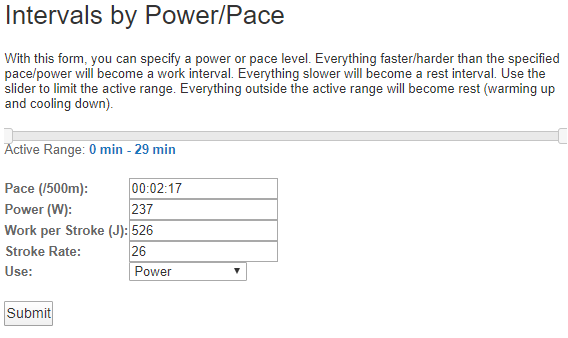
And then pick a slicing value. The page also includes a helpful flex plot to show you where your intervals exist and the current summary. Before you define intervals, it will look something like this.
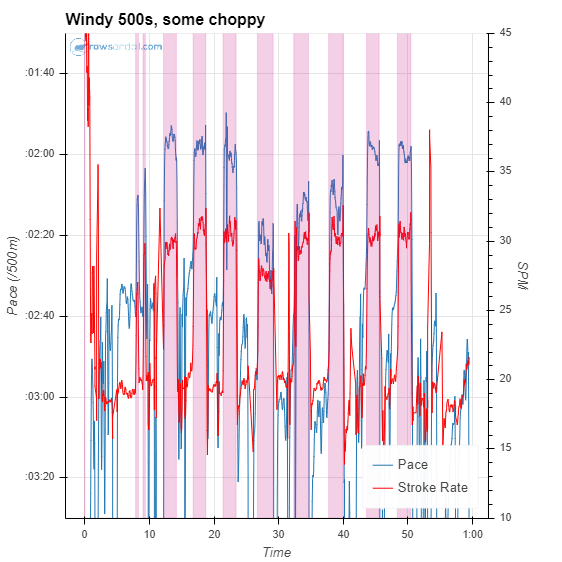
Rowsandall also comes up with suggested slice values. You can use them or decide on your own. I decided to try and slice this workout on a pace of 2:21. You type it into the form, select “pace” in the “use” box, and click submit.
After that, here’s what the plot looks like.
And this is the summary:
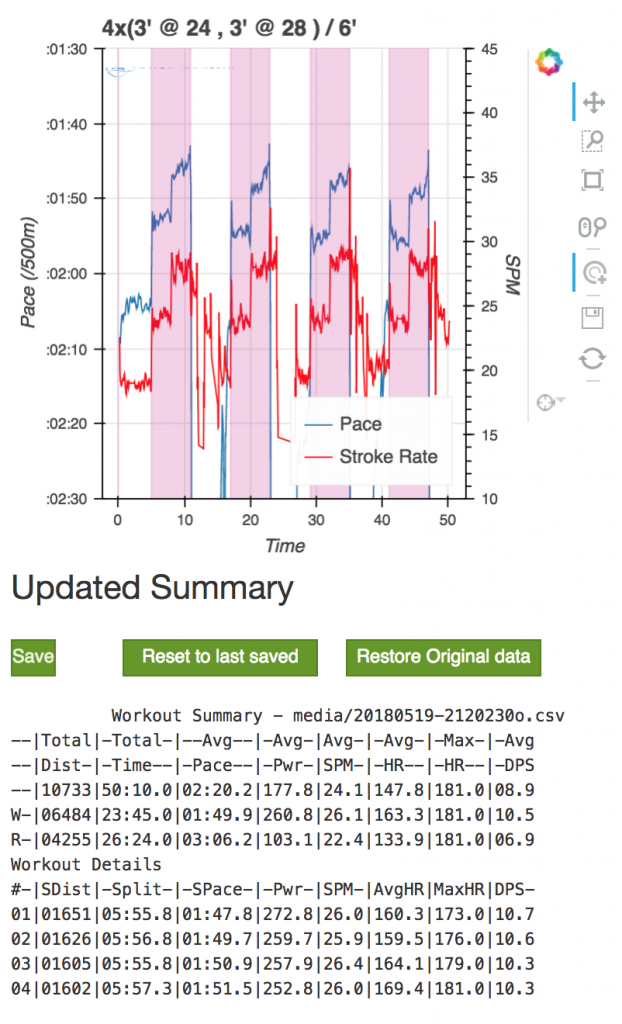
Workout Summary - media/20190616-1840460o.csv --|Total|-Total----|--Avg--|-Avg-|Avg-|-Avg-|-Max-|-Avg --|Dist-|-Time-----|-Pace--|-Pwr-|SPM-|-HR--|-HR--|-DPS --|10809|00:59:26.0|02:45.0|164.2|23.4|146.7|181.0|07.8 W-|03587|00:14:42.7|02:03.0|276.1|29.9|162.8|179.0|08.2 R-|07233|00:44:44.1|03:05.5|127.4|21.3|141.4|179.0|07.2 Workout Details #-|SDist|-Split-|-SPace-|-Pwr-|SPM-|AvgHR|MaxHR|DPS- 01|00081|00:21.6|02:13.5|246.0|24.9|144.5|151.0|09.0 02|00520|02:02.8|01:58.1|285.1|29.3|154.5|171.0|08.7 03|00514|02:01.8|01:58.5|285.9|30.5|163.8|175.0|08.3 04|00509|02:03.0|02:00.7|273.3|30.3|162.0|177.0|08.2 05|00101|00:27.7|02:17.4|269.8|27.8|162.4|166.0|07.8 06|00347|01:32.2|02:12.7|279.3|29.9|170.3|176.0|07.6 07|00477|02:04.6|02:10.6|285.7|30.3|168.0|179.0|07.6 08|00505|02:01.2|01:59.9|269.5|30.2|160.4|174.0|08.3 09|00532|02:07.8|02:00.0|262.2|30.1|165.5|177.0|08.3
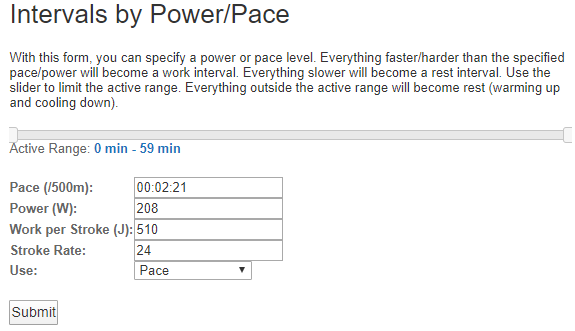
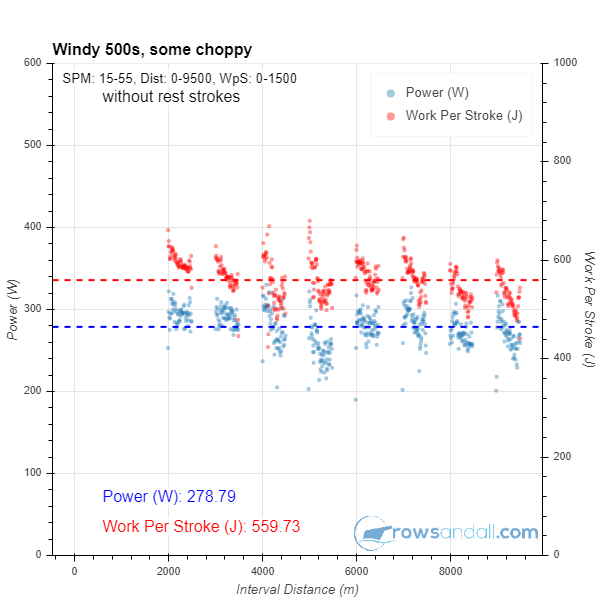
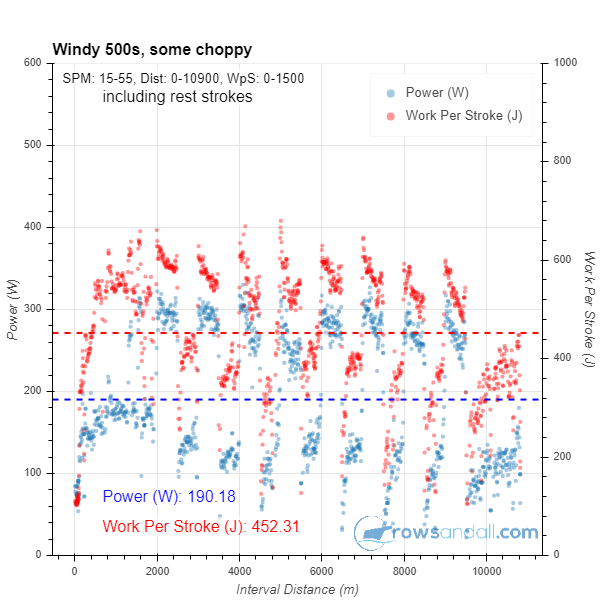
So, by slicing at this pace, intervals were defined for one of the bursts of the warming up (interval 01) and all of the 500m intervals (intervals 02 through 09). The line at the top, preceded by “W-” is a total of all the work intervals. The problem here is that by using Pace, I have missed part of the intervals 05 and 06, where I was rowing in headwind in pretty choppy water. If you have a power meter in the boat like I do, you generally get better results by slicing by Power. If you don’t, slicing by stroke rate is usually a good option.
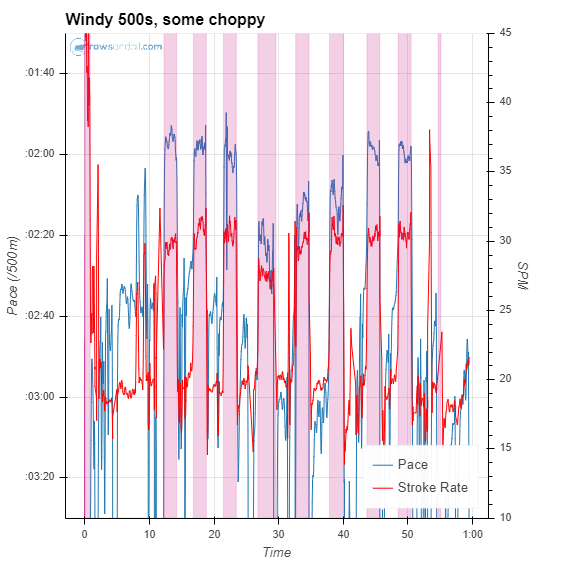
Sliced by Power:
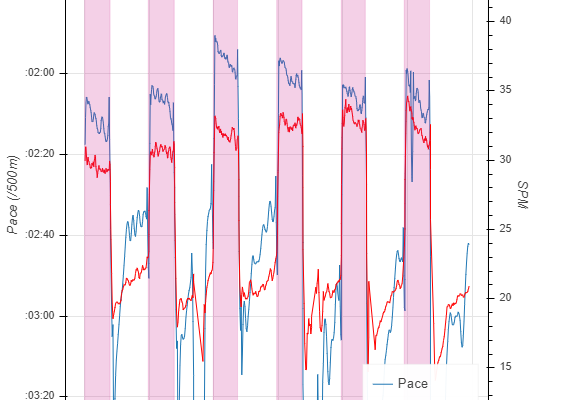
Or sliced by Stroke Rate:
The problem with slicing by stroke rate is that it catches some parts of the workout which were not the main intervals:
- Fixed seat paddling in the first few minutes
- A technical drill in the cooling down
For that, we have an active window slider:
For this workout, I have set it to start at 11 minutes (after my warming up) and end at 52 minutes (at the start of the cooling down). That filters out those high stroke rate drills.
After you are satisfied with how your intervals are sliced, remember to click save. Then you can go to other tools and analyze just the “work” portion of the workout. For example, here’s the flex plot, with and without rest strokes.
Of course, this new feature also works for erg sessions, like this one.
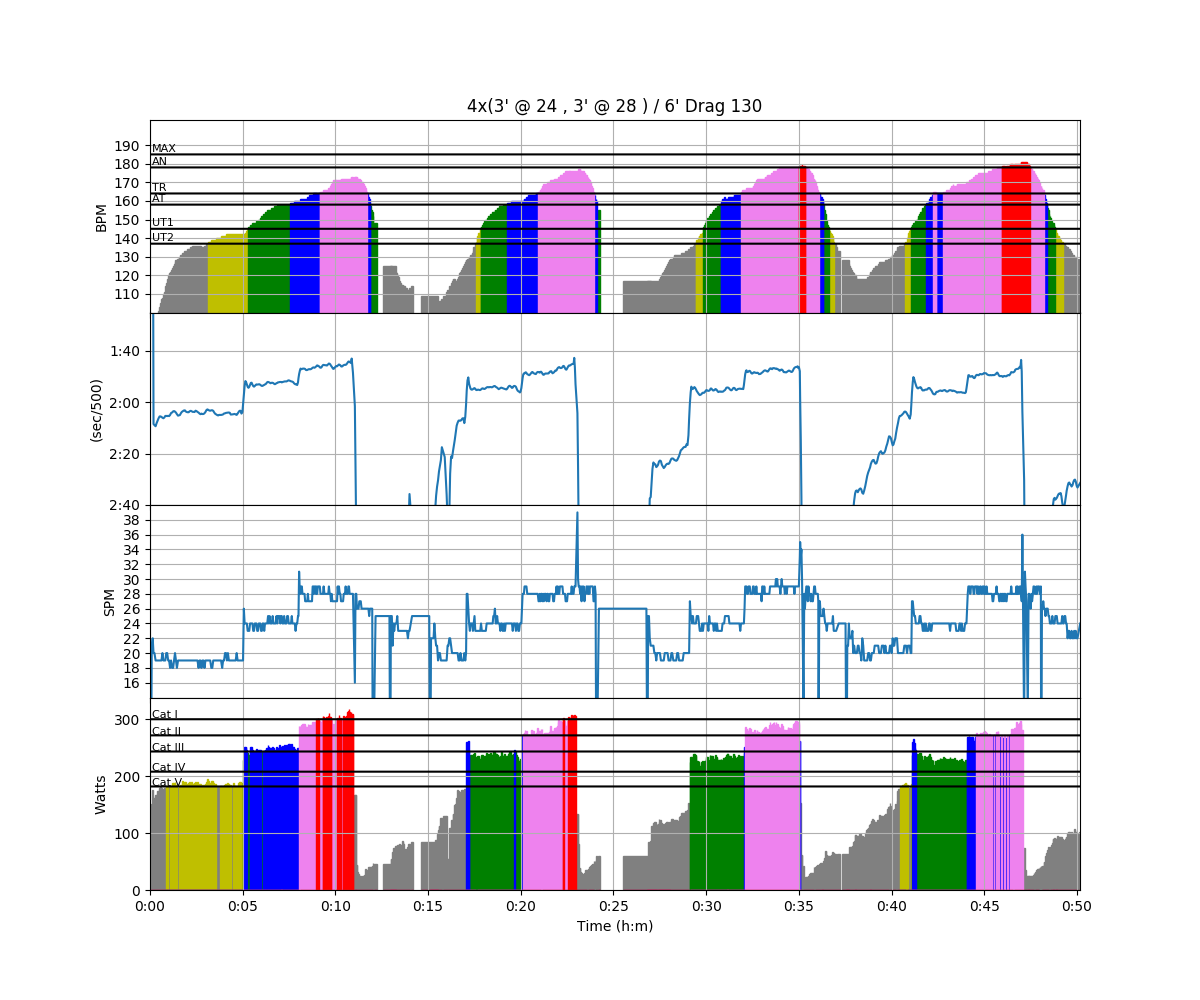
This workout was 5′ at r20, 3′ @ r24, and 3′ @r28. Using the interval feature, you can pick out just the r24 and r28 sections, using pace or power.
In this case, I sliced the workout using power and selected 210W as the slice value.
The result is this…
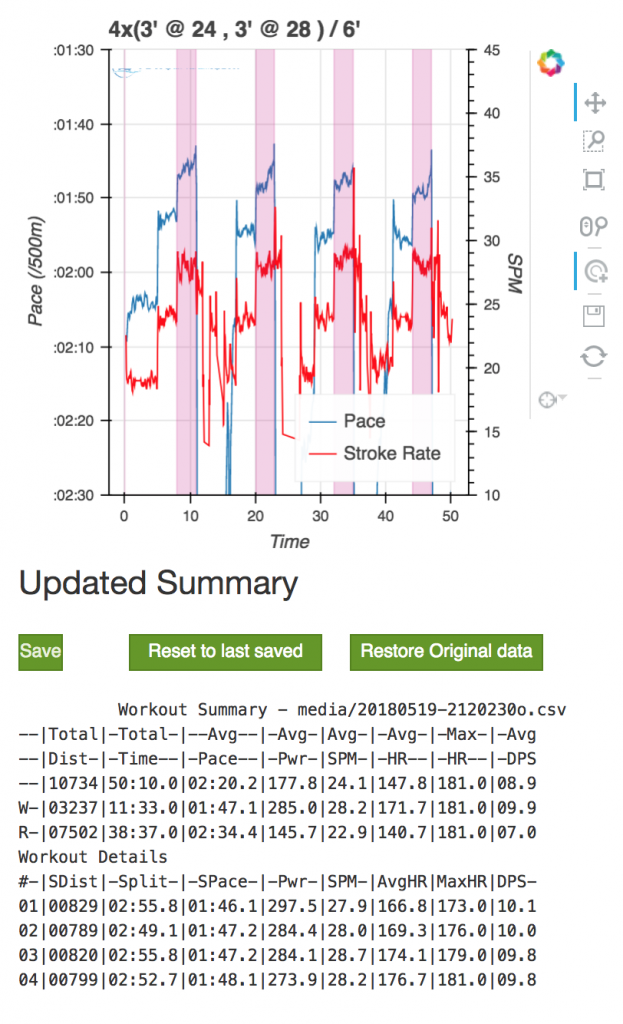
If I want to just focus on the r28 sections, I can redefine the slice value to 250W, and the result is this.
If intervals a part of your workout plan, this new feature makes it easier than ever to get useful insights from your training data, and allows you more flexibility when you are trying to do intervals safely on the water.
As always, if you have any questions, feel free to ask them in the comments section.